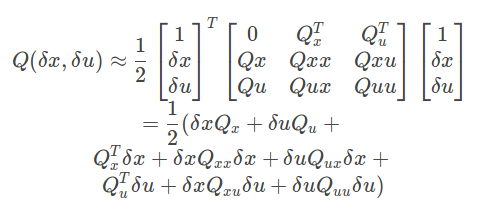（1）

Q(\delta x,\delta u)\approx \frac{1}{2} \begin{bmatrix}
   1 \\
   \delta x \\
   \delta u
\end{bmatrix}^T \begin{bmatrix}
   0 & Q_x^T & Q_u^T \\
   Qx & Qxx & Qxu\\
   Qu & Qux & Quu
\end{bmatrix} \begin{bmatrix}
   1 \\
   \delta x \\
   \delta u
\end{bmatrix}

\\

= \frac{1}{2} ( \delta x Q_x + \delta u Q_u + \\
Q_x^T \delta x + \delta x Q_{xx} \delta x + \delta u Q_{ux} \delta x + \\
Q_u^T \delta u + \delta x Q_{xu} \delta u + \delta u Q_{uu} \delta u )

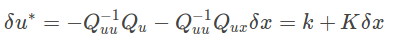（2）

\delta u^* = -Q_{uu}^{-1} Q_u -Q_{uu}^{-1} Q_{ux} \delta x = k + K \delta x

将 （2）式代入（1）式：

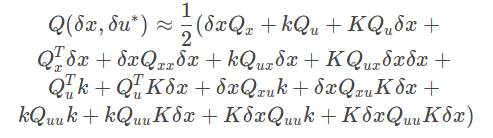
Q(\delta x,\delta u^*)\approx
\frac{1}{2} ( \delta x Q_x + k Q_u +K Q_u \delta x + \\
Q_x^T \delta x + \delta x Q_{xx} \delta x + k Q_{ux} \delta x + K Q_{ux} \delta x \delta x + \\
Q_u^T k + Q_u^T K \delta x + \delta x Q_{xu} k + \delta x Q_{xu} K \delta x + \\
 k Q_{uu} k + k Q_{uu} K \delta x + K \delta x Q_{uu} k + K \delta x Q_{uu} K \delta x )

分项整理得到：

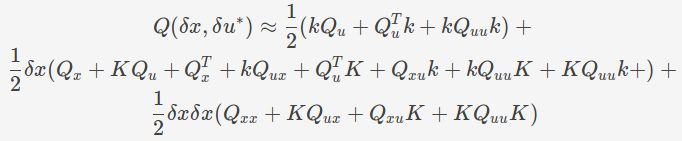
Q(\delta x,\delta u^*)\approx

\frac{1}{2} (k Q_u + Q_u^T k +  k Q_{uu} k ) + \\

\frac{1}{2} \delta x (Q_x + K Q_u + Q_x^T  +  k Q_{ux} + Q_u^T K +  Q_{xu} k +  k Q_{uu} K  +  K  Q_{uu} k +  ) + \\

\frac{1}{2} \delta x \delta x (Q_{xx} + K Q_{ux}  +  Q_{xu} K + K  Q_{uu} K ) 

第一项为：

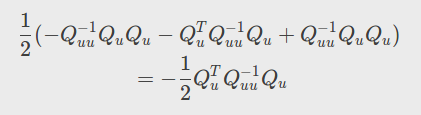
第二项为：

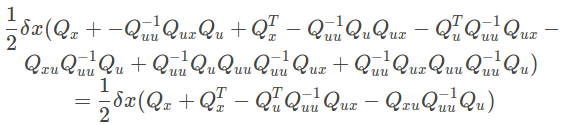
\frac{1}{2} \delta x (Q_x + -Q_{uu}^{-1} Q_{ux} Q_u + Q_x^T  -Q_{uu}^{-1} Q_u Q_{ux} - Q_u^T Q_{uu}^{-1} Q_{ux} -\\  Q_{xu} Q_{uu}^{-1} Q_u +  Q_{uu}^{-1} Q_u Q_{uu} Q_{uu}^{-1} Q_{ux}  +  Q_{uu}^{-1} Q_{ux}  Q_{uu} Q_{uu}^{-1} Q_u )\\
= \frac{1}{2} \delta x(Q_x + Q_x^T - Q_u^T Q_{uu}^{-1} Q_{ux} -Q_{xu} Q_{uu}^{-1} Q_u )

第三项为：

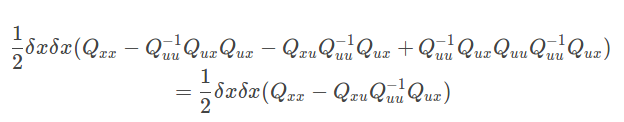
\frac{1}{2} \delta x \delta x (Q_{xx} -Q_{uu}^{-1}Q_{ux}Q_{ux} -Q_{xu}Q_{uu}^{-1}Q_{ux}
+ Q_{uu}^{-1}Q_{ux}Q_{uu}Q_{uu}^{-1}Q_{ux} ) 
\\
=\frac{1}{2} \delta x \delta x (Q_{xx}-Q_{xu}Q_{uu}^{-1}Q_{ux} ) 

链接：

https://www.matheditor.cn/#environments

https://latex.91maths.com/